Der Klirrfaktor bei einer Arbeitskennlinie von komplizierterer Form 1)

Die Homepage von H.-T. Schmidt

¹) W. KLEEN, Kennlinienfelder, Leistung und Verzerrung von Verstärkerröhren, insbesondere Endröhren. Telefunkenröhre 1934, 58. Heft 2.

Arbeitskennlinien von der in Abb. 205 gezeigten Form lassen sich angenähert durch eine Gleichung n-ten Grades darstellen. Begnügt man sich mit 3 oder 4 Harmonischen, was praktisch in den meisten Fällen ausreicht, so kommen wir mit einer Gleichung vom 3. oder 4. Grade aus. Aus Symmetriegründen wählen wir eine Gleichung 4. Grades, gehen also von dem Ansatz ia = a + bx + cx2 + dx3 + ex4 (65) wo x zwischen +1 und -1 schwankt, aus, und ermitteln aus der nachstehenden Arbeitskennlinie ia = f(x) (Abb. 205) die Konstanten a, b, c, d, und e. Dazu sind fünf Gleichungen erforderlich. Diese erhalten wir aus (65): Für  x =  0  ist  i0  = a }   für  x =  +1  ist  i+1  = a +  b  +  c  +  d  +  e   für  x =  −1  ist  i−1  = a −  b  +  c  −  d  +  e für  x =  +½  ist  i+½  = a +  b  +  c  +  d  +  e 2 4 8 16 für  x =  −½  ist  i−½  = a −  b  +  c  −  d  +  e 2 4 8 16 (66) Hieraus ergeben sich die Konstanten a, b usw. zu: a =  i0 }   b =  4 ( i+½ − i−½ )  −  1 ( i+1 − i−1 ) 3 6 c =  −5 i0 +  8 ( i+½ + i−½ )  −  1 ( i+1 + i−1 ) 3 6 d =  2 ( i+1 − i−1 )  −  4 ( i+½ − i−½ ) 3 3 e =  2 ( i+1 + i−1 )  −  8 ( i+½ + i−½ )  +  4 i0 3 3 (67)

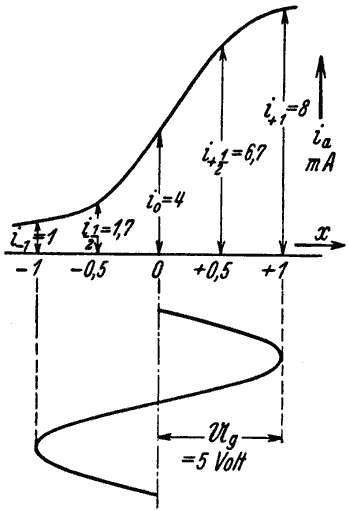
Abb. 205. Zur Ermittlung des Klirrfaktors einer Arbeitskennlinie von komplizierterer Form.

Setzen wir nun in (65) wieder

x = sin ωt

(68)

und lösen die Potenzen von sin ωt in der in (56) gezeigten Weise auf, so erhalten wir den Gleichstrom und die Amplituden der Harmonischen nach (57) und (67) zu

Ia  =  i+1 + i−1  +  i+½ + i−½ 6 3 Ja1  =  i+1 − i−1  +  i+½ − i−½ 3 3 Ja2  =  i0  −  i+1 + i−1 2 4 Ja3  =   −  i+1 − i−1  +  i+½ − i−½ 6 3 Ja4  =  i0  +  i+1 + i−1  −  i+½ + i−½ 2 12 3

(69)

wobei die fünf Ordinaten (i_o, i₊₁, i_-1 usw.) der Arbeitskennlinie in der in Abb. 205 gezeigten Weise zu entnehmen sind. Mit den vorstehenden Konstanten ergibt sich die Gleichung des Anodenstromes i_a = f(t) entsprechend (54c) zu:

ia  =  Ia  +  Ja1  sin ωt +  Ja2  cos 2 ωt +  Ja3  sin 3 ωt +  Ja4  cos 4 ωt

(70)

Dieser Strom hat nach (58a) einen Klirrfaktor von

K =  √ Ja22 + Ja32 + Ja42 Ja12

(71)